Rechercher un outil (en entrant un mot clé):
Calculer la moyenne harmonique H
La moyenne harmonique pondérée d'une série de n valeurs x_1, x_2, ... , xn dont les poids respectifs (ou coefficients) est la suite de nombres suivante : p_1, p_2, ... ,pn , est donnée par la formule :
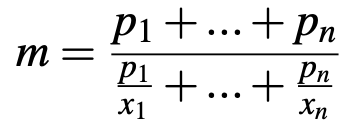
ou encore si tous les poids sont égaux la moyenne harmonique devient :
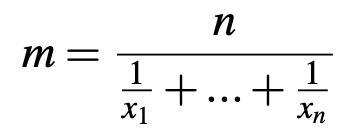
Moyenne de deux vitesses sur un même trajet
Pourquoi la vitesse moyenne d'un trajet aller/retour n'est pas la moyenne arithmétique des vitesses aller et retour.
Lors d'un trajet aller/retour la distance aller (notée `d`) et la distance retour sont par définition identiques, ainsi la distance aller/retour est égale à `D = 2 times d`
Notons les durées (différentes) des deux trajets `t_1`et `t_2` et leurs vitesses respectives : `v_1`et `v_2`
On a : `v_1 = d/t_1` et `v_2 = d/t_2` ainsi `t_1 = d/v_1` et `t_2 = d/v_2`
Avec ces notations, la vitesse moyenne du trajet complet est égale par définition à :
`V_m = D / ( t_1+ t_2 )`
`V_m = (2d) / ( d/v_1 + d/v_1 )`
`V_m = 2 / ( 1/v_1 + 1/v_1 )` on reconnait ici la moyenne harmonique de deux valeurs.
Moyenne harmonique de deux valeurs
La moyenne harmonique de deux valeurs `v_1` et `v_2`, est donnée par la formule suivante :
`V = (1+1)/(1/v_1 + 1/v_2)`
`V = 2/(1/v_1 + 1/v_2)`
`V = 2/(v_2/(v_1v_2) + v_1/(v_1v_2))`
`V = (2v_1v_2)/(v_2+v_1) (F_1)`
Cette formule donne la vitesse moyenne lorsqu'on effectue deux fois la même distance (par exemple aller/retour) à des vitesses différentes.
Moyenne d'un aller/retour d'un trajet en avion
Vous effectuez le même trajet 2 fois en avion (classiquement un aller retour) ; la première fois à une vitesse de 780 km/h et la seconde fois à une vitesse de 880 km/h. Quelle a été la vitesse moyenne de votre voyage ?
Une réponse très rapide serait `(780+880) / 2 = 830` km/h, mais c'est une réponse fausse.
En effet, le second trajet s'est effectué en moins de temps que le premier.
Vous avez donc volé moins longtemps à la vitesse la plus élevée.
Notons `d` la distance d'un trajet. La distance totale effectuée lors des 2 trajets est donc égale à `D = 2 times d`. Notons `t_1` la durée du premier trajet et `t_2` la durée du second trajet.
Ainsi nous obtonons les relations suivantes :
`780 = d/t_1` et `880 = d/t_2`
De là `t_1 = d/780` et `t_2 = d/880`
La vitesse moyenne est égale à : `V_m = D/T` avec `T = t_1 + t_2`
`V_m = D / ( t_1+ t_2 )`
`V_m = (2d) / ( d/780 + d/880 )`
`V_m = 2 / ( 1/780 + 1/880 ) \approx 826.988`
Où en utilisant la formule `(F_1)`, `V_m = (2 times 780 times 880)/(780+880)\approx 826.988`
La moyenne réelle s'élèvent de 827 km/h.
Ce qu'il faut retenir :
- pour effectuer la moyenne de plusieurs vitesses (sur une même distance) il faut utiliser la moyenne harmonique.
- plus l'écart entre les vitesses aller et retour est important, plus la différence entre la vitesse arithmétique et la vitesse harmonique (la moyenne réelle) est importante. (voir exemple suivant)
Moyenne d'un trajet à pied et à vélo.
Vous effectuez un trajet de 4 km, l'aller à pied en 1 heure, soit 4 km/h et le retour à vélo à 20 km/h.
Moyenne arithmétique :
`(4+20)/2 = 12`
Moyenne harmonique :
`2/(1/4 + 1/20)= 2/(5/20 + 1/20) = 2/(6/20) = 40/6 \approx 6.67`
La moyenne réelle est de 6,67 km/h !
Le trajet à vélo a été effectué en 0,2 heure soit 12 minutes, beaucoup plus rapidement qu'en marchant.
`t = d/v = 4/20 = 0.2`

